Enlarge on Calculations of Present Value Formulas in Excel for Continuous Compounding & Perpetuity

We will talk about the rest of PV in this article to complete all previously mentioned. As usual, we use Microsoft Excel to mathematically calculate the formulas or to insert Function to return the solution. Moreover, we will enlarge on the certain formulas by proving the different forms around the bottom of the page or in the link file. Logarithm is also used to calculate the number of the years in the financial formula.

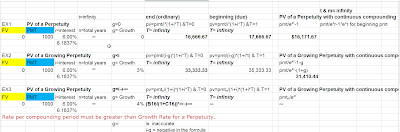
As below, I provide you the picture with the description and the link file to each item. Also note that the two new functions have been used in the link files: EXP and Seriessum.

1 PV of a Future Sum with Continuous Compounding:

2 PV of an Annuity with Continuous Compounding:

3 PV of a Growing Annuity with ContinuousCompounding (g ≠ i):

4 PV of a Growing Annuity with ContinuousCompounding (g = i):

5 PV of Combined FV and Cash Flow with ContinuousCompounding:

6 PV of a Perpetuity & PV of a Perpetuity withContinuous:

7 PV of a Growing Perpetuity (g < i) & PV of a Growing Perpetuity (g < i) with Continuous Compounding: See item 6.

8 PV of a Growing Perpetuity (g = i) & PV of a Growing Perpetuity (g = i) with Continuous Compounding: See item 6.

Out of the normal PV with compounding, there is the remainder from the previous post worth mentioning, i.e. the formula about PV ofCombined FV and growing cash flow with compounding (g ≠ 0) and the formula of Uneven Cash flow withcompounding.

Check the details inside the link to see what formulas are used and to know how to use NPV function.

Prove the different forms to the formula of an Annuity with Continuous Compounding and to the formula of a Growing Annuity with Continuous Compounding

Two forms to each formula have been found from the web sites so we need to know the difference between them for the same content. The tests are proven in the link files above for the same contents.

A) An Annuity with Continuous Compounding:

(pmt/e^r-1)*(1-1/e^rt)  Vs  pmt*(1-1/e^rt)/r Just edit r to (1+r/m)^m-1 close to e^r-1 due to Cont. Comp. interest.

B) A Growing Annuity with Continuous Compounding:

(Pmt*e^-g/e^(r-g)-1)*(1-e^-(r-g)t) Vs    (pmt/(e^r-1-g))*(1-(1+g)^t/e^rt)

See the step by step test accompanied the how-to calculation in the link file above or see the brief test below.

((Pmt/e^g)*(1/e^r/e^g-1))*(1-e^-(r-g)t)
((Pmt/e^g)*(1/(e^r-e^g)/e^g))*(1-e^-(r-g)t)
((Pmt/e^g)*(e^g/(e^r-e^g)))*(1-e^-(r-g)t)
pmt/e^r-e^g*(1-e^-(r-g)t)
Given e^g = (1+g) moves to (1+g/m)^m
then
(pmt/e^r-(1+g))*(1-(e^gt/e^rt))
(pmt/e^r-1-g)*(1-(1+g)^t/e^rt))

How to Use Logarithm for Finding n Period

To know the rule of log and power is useful to understand some complicated calculations around this article, particularly in this sub heading.

Rule of Log				Rule of Power
log(2*3)= log(2)+log(3)				2^(2+3) = 2^2*(2^3)
0.77815	0.77815	>power of base 10		32	32
log3(4/5)= log3(4)-log3(5)				2^(2-3)=  2^2/2^3
-0.2031	-0.2031	>power of base 3		0.5	0.5
2log(x) =log(x^2)

Log Calculation for PV of future sum with continuous compounding: Given PV= 657.0468198, FV= 1000, r= 6% Find the answer for n period (the number of years for making FV= 1000 worth PV= 657.0468198).

Logarithm's calculation
PV=FV/(e^rt-1+1)
e^rt= FV/PV
log (e^rt) = log(FV/PV)
rt*log(e) = log (FV/PV)
6%*t *log(2.7182818284) = log (1000/657.05)
6%*t *log(2.7182818284) =		0.605932
6%*t =		0.42
t =		7

As for this last paragraph, I provide all of you the link of online calculator and the link of wikipedia’s time value of money for present value in order to see more information, calculate the numbers, and review the raised points altogether.